#1 Walk Around Earth

Yes!! It is possible. And in infinitely many ways actually.

The first way is in my opinion the most trivial one: Start at the north pole.

Your distance to the poles always stays the same when you're going east/west (since you are walking in a circle along the same latitude). This means that if you were to start your journey at the north pole you would be one kilometer south of the north pole after the first kilometer (trivially), after the second kilometer you would still be one kilometer south of the north pole (only in a different location), and after walking one kilometer north to complete the journey you would be back at the north pole, just like what we wanted.

The second way to do it is to start one kilometer north of the south pole.

In this scenario we exploit the fact that there is no east on the south pole (this is also the most iffy solution since you're never really walking east at all). After your first kilometer you are at the south pole. Then you walk one kilometer east on the south pole (do nothing) and then you walk back to your starting point (note that you could have actually walked north to some other point, but that isn't too useful for us).

The rest of the ways to do it all follow a similar pattern. We will start with the easiest one: Start anywhere on the circle that's one kilometer north of the circle (of latitude) that's one kilometer in circumference.

I know this one was a little wordy. I hope this image can help: 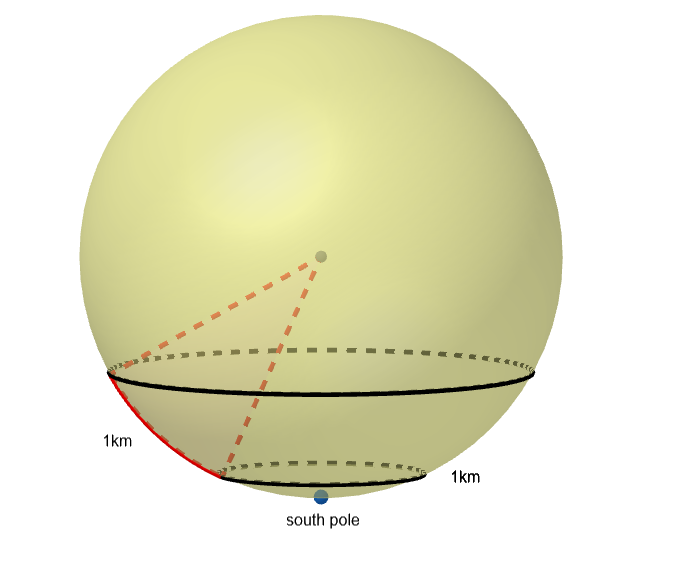(In the image it's any point on the top circle you should stand on)

This works because after walking one kilometer east on the lower circle you will end up on the same point. So you are basically walking one kilometer south, one lap around the circle of latitude you're on and finally one kilometer north back to the same point as you started.

The infinite solutions comes from extending this last one. Instead of walking one lap around the circle of latitude we could walk any whole number of laps. In other word we would need to start anywhere on the circle that is one kilometer north of the circle with circumference 1000/n meters for any positive integer n. (this actually (kinda) includes the second example where we walked to the south pole and back if we let n go to infinity)

That's all the possibilities i could think of, I hoped you enjoyed solving this little problem and that you may come back for the next one.

If you're thinking about the possibility of walking laps around circles of latitude on the northern hemisphere. There is an easy way to intuitively understand that it's not possible:

The smallest possible circle of latitude you could get to on the northern hemisphere is the one that is exactly one kilometer south of the north pole. Since walking one kilometer south (along a great circle) won't affect the curvature of the earth much we will consider the earth around the north pole as a flat plane. Then the circumference of this smallest circle will be 2πr = 2π * 1 = 2π kilometers. We only walk one kilometer east so we won't be able to make a single lap around this circle even though it's the smallest circle we can possibly get to, hence we can't lap any circle on the northern hemisphere.